Автор: Дюков Михаил, 17 лет
Руководитель: Бондарь Ольга Святославовна
педагог дополнительного образования, методист
ГБУ ДО ЦДЮТТ Московского района Санкт-Петербурга
Работа удостоена диплома I степени на Всероссийской конференции с международным участием «Школьная информатика и проблемы устойчивого развития», 2021 г.

Сущность математики в том, что человек учится видеть различные варианты решения одной и той же задачи, умеет ставить перед собой задачи и находить на них ответы, ищет доказательства и аргументы. Без числовых последовательностей, закономерностей и способов решения детский ум не способен решать ни абстрактные ни конкретные задачи. Это касается любой области знаний: физика, химия, биология, даже, гуманитарные дисциплины как история и русский язык – это теория логических систем, которые лучше всего усваиваются именно на примерах математики. Развитие интеллектуальных способностей человека приводит к тому, что он начинает хорошо ориентироваться и в других дисциплинах, там, где требуются эти же навыки. Фактически можно сказать, что математика — это основа человеческого интеллектуального потенциала или, как говорили древние – «царица наук».


Для оформления своей работы (фон для анимации, тематика задач) я взял космическую тематику. Тему космоса я выбрал не случайно. Во-первых, 12 апреля 2021 года исполняется 60 лет со дня первого полета человека в космос. Во-вторых, тема космоса напрямую связана с математикой. Человечество в течение уже не одного столетия пытается исследовать космос: другие планеты, солнечные системы, галактики. Со временем возникают новые научные дисциплины, входящие в состав астрономии, изучающие свойства и эволюцию Вселенной в целом. Основу таких дисциплин составляет математика, физика и астрономия. Все естественные науки на основе наблюдений закономерностей выдвигают теории и гипотезы, но большинство из них могут быть доказаны только математическими расчетами. Для космических проектов и наблюдений с первых шагов освоения космического пространства необходимо было разрабатывать методы решения математических задач. Уже не одно поколение людей занимается исследованием космоса. Законы движения планет Солнечной системы основаны на математических законах Иоганна Кеплера – великого немецкого ученого начала XVII века. Древнегреческий ученый Гиппарх в 150 г. до н.э. составил первый звездный каталог. Гиппарх разделил все видимые звезды на 6 групп, наиболее яркие отнес к «звездам первой величины». Шкала звездных величин – логарифмическая. Формула Погсона позволяет определить блеск светил, вычислить их истинную светимость, а показатели цвета – температуру и геометрические размеры звезд. Одно из важнейших свойств космического пространства – это цикличность происходящих в ней процессов. Математика всегда помогала развитию других наук, и сама развивалась под их воздействием.
Рене Декарт, писал: «К области математики относят науки, в которых рассматриваются либо порядок, либо мера, и совершенно не существенно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое…; таким образом, должна существовать некая общая наука, объясняющая все, относящееся к порядку и мере, не входя в исследование никаких частных предметов».
Несмотря на простоту ранних вычислительных устройств, опытный счетовод может получить результат при помощи простых счетов даже быстрее, чем нерасторопный владелец современного калькулятора. Естественно, производительность и скорость счета современных вычислительных устройств уже давно превосходят возможности самого выдающегося расчетчика-человека.
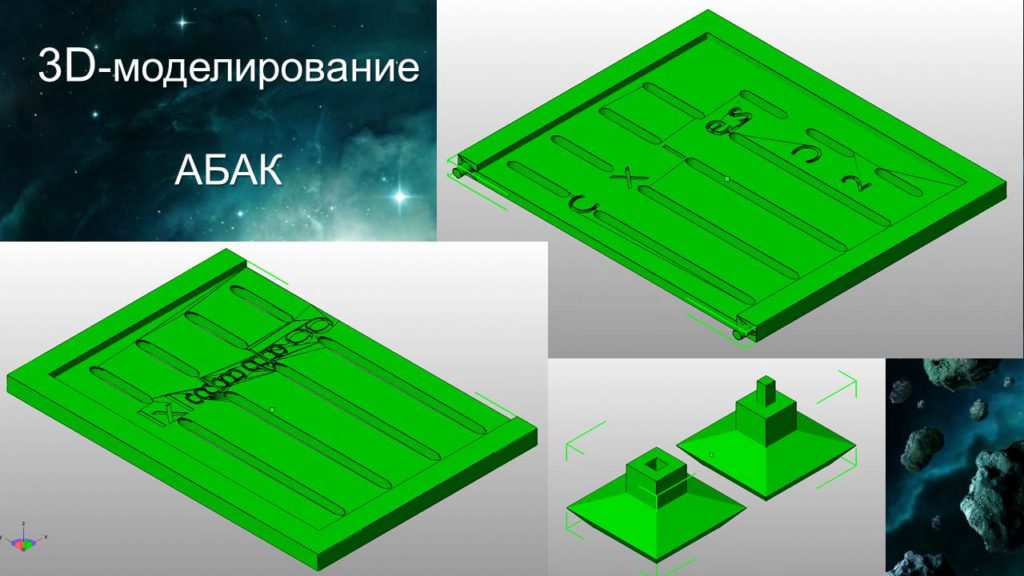
В Древнем Риме абак появился, вероятно, в V–VI веках. Римские абаки изготавливались из различных материалов (бронза, слоновая кость, цветное стекло). Бронзовый римский абак, хранящийся в Национальном археологическом музее Неаполя, представляет собой доску с прорезанными в ней щелями, в которых перемещаются костяшки.
Над длинными щелями помечены значения разрядов: миллионы, сотни тысяч, десятки тысяч, тысячи, сотни, десятки, единицы, унции (то есть двенадцатые части). В щели, помеченной « », – пять костяшек (то есть 5/12). В правой части абака — щели с пометками, означающие 1/2, 1/4 и 1/6 унции.
Распад и падение Римского государства прервали развитие счетной техники. Абак в Европе был надолго забыт.
В Китае аналог абака – суаньпань – появился в VI веке и постепенно вытеснил традиционную систему счета на палочках. Со временем его устройство менялось, современный вид он приобрел в XVII веке. Суаньпань представляет собой прямоугольную раму, разделенную на две части. В большом отделении («Земля») на каждой проволоке – 5 шариков, в меньшем («Небо») – 2 шарика. Проволоки соответствуют десятичным разрядам, каждый шарик большего поля – единице, меньшего – пяти. На суаньпане можно не только производить четыре арифметических операции, но и извлекать квадратные и кубические корни.
В XV–XVI веках суаньпань был завезен в Японию, где получил название «соробан». В Японии он был модифицирован (последний раз – в 1930 году).
Абак, забытый в Европе после распада Римской империи, вновь получил распространение в X веке благодаря монаху Герберту Орильякскому (938–1003), ставшему впоследствии римским папой Сильвестром II. Герберт во время путешествия в Кордовский халифат познакомился с арабской системой цифр и с абаком.
В XV веке в Англии появилась новая форма абака – «счет на линиях», распространившаяся в XV–XVI веках по континентальной Европе. Для счета на линиях использовались горизонтально разлинованная доска и металлические жетоны, которые в Германии назывались счетными пфеннигами, в других странах – фишками. Жетоны при счете выкладывались не только на линиях, но и между ними. Разрядность повышалась снизу-вверх.

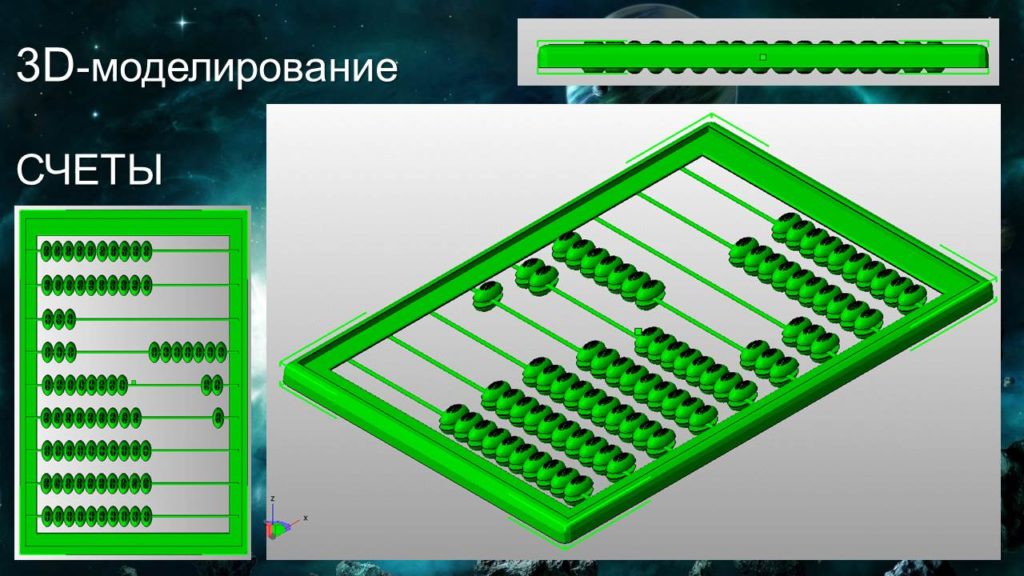
Принцип эквивалентности широко использовался в счётном устройстве — абаке, или счётах. Количество подсчитываемых предметов соответствовало числу передвинутых костяшек этого инструмента.
В России существовал аналогичный счету на линиях способ, называвшийся «счет костьми». Он описан в рукописных книгах XVI века, объединенных общим названием «Цифирная счетная мудрость», но возник задолго до этого. Свое название способ получил из-за использования для счета сливовых или вишневых косточек. Внешне приспособление напоминало европейскую доску для счета на линиях. Горизонтальные линии служили разделителями разрядов. Косточки на линиях обозначали единицы разряда, кость над линиями — пять единиц разряда. Иногда для счета служили металлические жетоны («пенязи», что дало второе название — «счет пенязями»). Для вычисления налогов на досках применялись добавочные разделения для подсчета трети (1/3), полутрети (1/6) и так далее до «малой чети» (1/32).
В XVI веке на смену счету костьми пришел более удобный «дощаный счет». Его полное описание содержится в списке «Счетной мудрости» 1691 года. Первоначально устройство для дощаного счета представляло собой два соединенных ящика, каждый из которых был разделен на два отделения. Наличие четырех отделений позволяло не только сохранять условие задачи, но и фиксировать промежуточные расчеты. В каждом отделении было натянуто по 14 веревочек с нанизанными на них костяшками. На верхних десяти было по 9 костяшек (иногда — по 10), они предназначались для операций с целыми числами. На нижних рядах, содержащих 3, 4, 5 или 6 косточек, производились операции с дробями. Ряды с одной или двумя костяшками представляли половину той дроби, под которой они находились.
Постепенно устройство дощаного счета совершенствовалось, в нем стали применяться только две части вместо четырех, и только нижние ряды, для работы с дробями, имели четыре отделения. Затем исчезли ряды, содержащие по одной костяшке.
В XVII веке меняется название прибора, в 1658 году «счоты» впервые упоминаются в «Переписной книге домовой казны патриарха Никона». В начале XVIII столетия дощаный счет в России окончательно трансформируется в «счеты», в дальнейшем претерпевая только незначительные внешние изменения. В XIX веке русские счеты стали известны в Западной Европе, однако использовались там только для обучения в начальной школе. В России они применялись в торговле и бухгалтерском учете до конца XX века, пока не были окончательно вытеснены калькуляторами. В начальной школе для обучения счету они служили до конца 1980-х годов.
В счетах применяется позиционная десятичная система счисления. Каждый ряд костяшек представляет собой числовой разряд, возрастающий от единиц до сотен тысяч, а вниз — уменьшающийся от десятых до тысячных. Прут с четырьмя костяшками служит разделителем целых и дробных частей, а также для счета полушками (1/4 копейки).


Также я решил украсить боковые части юпаны и внутренний ящичек рельефами с изображениями культовых персонажей, встречающимися на предметах с декоративным оформлением. Так, на одном из глиняных сосудов я увидел рельеф ворона. Ворон — символ мудрости у большинства народов. Его я скопировал на внутреннюю часть ящичка юпаны.
Для создания рельефов я использовал программу векторной графики CorelDRAW. В программу CorelDRAW я загружал изображения, взятые в интернете, и отрисовывал их инструментом «форма». После сохранял рисунок в формат .svg. Данный формат легко импортируется в Blender и уже, непосредственно, в Blender, я переводил кривые в 3D-объект.

После перевода моделей в нужный формат, был сгенерирован «.gcode» в программе Poligon. Poligon тоже — свободная программа.
Печатались модели в 3D-лаборатории Центра технического творчества Московского района Санкт-Петербурга на 3D-принтере Picaso, разработанным и созданным в России. Печатались модели пластиком — полилактидом. Это биоразлагаемый, биосовместимый, термопластичный, алифатический полиэфир, мономером которого является молочная кислота. Сырьем для производства служат ежегодно возобновляемые ресурсы, такие как кукуруза и сахарный тростник. Используется для производства изделий с коротким сроком службы, а также в медицине, для производства хирургических нитей и штифтов.
На печать каждой детали в среднем уходило по 4-5 часов. Также модели иногда получались бракованными из-за особенностей подготовки моделей к печати или сбоя принтера. Для того, чтобы напечатать абак размером 350×180мм (по внешним размерам), пришлось разделить модель на две части, так как размер печатного стола 200х200мм. Абак я немного переделал, настроив скрепление деталей при помощи пазов. Также для абака было напечатано 40 «косточек», тоже состоящих из 2 частей каждая. Юпана состоит из 3 частей: нижней части, коробочки для семян маиса и крышки.

Для оформления анимации я создал фон на космическую тематику: текстуру звездного неба и планеты. Такой фон очень красивый, размеренное движение планет не будет отвлекать от основной демонстрации счета.


Кратко рассказал об истории задействованных вычислительных устройств. Показал ролик (3D-анимация) как использовать счеты, абак и юпану. Потом повторил вычислительные действия на устройствах, используя модели. После предложил ребятам задачи по космической тематике.
На занятии ребята заинтересовались исторической справкой. Они с увлечением решали задачи с использованием смоделированных счетных устройств. Наибольший интерес вызвали счеты, как самый простой и понятный инструмент из предложенных.
В результате всем понравилось считать на счетах, 60% заинтересовались счетом на абаке и только 10 % — на юпане. 40 % хотели бы продолжить осваивать счеты. 80% школьников хотели бы познакомиться с другими историческими счетными устройствами. 35% хотели бы осваивать 3D-моделирование.

На занятии ребята также заинтересовались исторической справкой. Они тоже с увлечением решали задачи с использованием смоделированных счетных устройств. И снова наибольший интерес вызвали счеты. В следующий раз надо начать с юпаны или с абака, так как к рассмотрению третьего устройства ребята немного устают и внимание тоже немного ослабевает.



Найден способ подачи материала для обучения с увлечением школьников младших классов вариантам использования вычислительных устройств.
Удалось разработать 3D-модели счетных устройств для 3D-печати и распечатать их на 3D-принтере, а также создать обучающие ролики в технике 3D-анимации.
Привлекательная анимация способов счета знакомит ребят не только с вычислительными устройствами, но и с темой «космос». Так как в этом году мы отмечаем 60-летие первого полета человека в космос, для оформления анимации и для заданий были использованы элементы космической тематике.
Умение пользоваться счетными устройствами — полезный навык для детей младшего школьного возраста, так как воспитываются такие качества ума, как точность, чёткость и ясность, развивается логическое мышление, формируется гибкость ума, для ребят это возможность «потрогать» числа — все эти разряды, состав числа и прочие вещи, которые в школе не всегда даются легко. Также важно считать на разных устройствах, чтобы думать, искать и проверять разные варианты, понимать, что правильных решений может быть несколько. Проблема в сложных задачах зачастую не в том, чтобы вычислить правильно, а в том, чтобы понять — что с чем складывать. Если у ребят возникнет интерес, значит им легче будет учиться не только по математике, надеюсь, это поспособствует развитию логики, воображения. Надеюсь, знание приемов счета поможет им в разных жизненных ситуациях. А кого-то заинтересует 3D-творчество.
АНИМАЦИЯ СЧЕТА НА СТАРИННЫХ УСТРОЙСТВАХ
Демонстрация возможностей и принципы работы старинных устройств для счета: https://drive.google.com/drive/folders/1YXNVKenJuwMpGb1xxyo9gPo_LqlndA5s?usp=sharing

